
▮ 研究成果概要
北海道大学大学院 総合化学院 量子化学研究室の堤拓朗(リーディングプログラム3期生)は、北海道大学大学院 理学研究院数学部門 荒井迅准教授(現中部大学創発学術院教授)との共同研究によって、化学反応の理論的な解析に用いられる反応経路やそのネットワークを数理科学的手法に基づいて可視化する手法を定式化し、研究成果をJournal of Chemical Theory and Computationに発表しました。反応経路とは反応物、遷移状態、生成物をつなぐ座標空間内の一次元の経路であり、反応経路ネットワークとは同じ組成の分子の多数の安定構造が反応経路によって結ばれたネットワークです。反応経路ネットワークを図で示す場合、従来は安定構造および遷移状態構造が適当に配置された二次元図が使われてきましたが、本研究では「古典的多次元尺度構成法」を適用することにより、反応経路ネットワークに含まれる構造間の類似度が保持された反応経路地図の作成を可能にしました。本手法は原理的にはどのような化学反応に対しても適用可能であり、1次元反応経路の幾何学的な特徴や多数の安定構造・遷移状態構造を含む反応経路ネットワーク全体の描像に対するより深い洞察を得ることが期待されます。
▮ 背景
一般に化学反応は素反応に分解することができます。素反応は一つの安定構造から出発してエネルギー的に不安定な遷移状態構造を経由し、別の安定構造に至る過程であり、数学的には座標空間内でこれら3つの構造をつなぐ一次元の経路として定義されます(これを反応経路と呼びます)。量子化学計算に基づく化学反応機構の議論では、ポテンシャルエネルギー曲面上に定義される反応経路として固有反応座標(IRC: intrinsic reaction coordinate)(※1)が重要な役割を果たしています。素反応に対して固有反応座標を求め、固有反応座標に沿った分子構造の変化やエネルギー変化を解析することにより、反応物の安定構造から遷移状態構造を経て生成物の安定構造に至る化学反応過程を直観的に理解することができます(図1)。
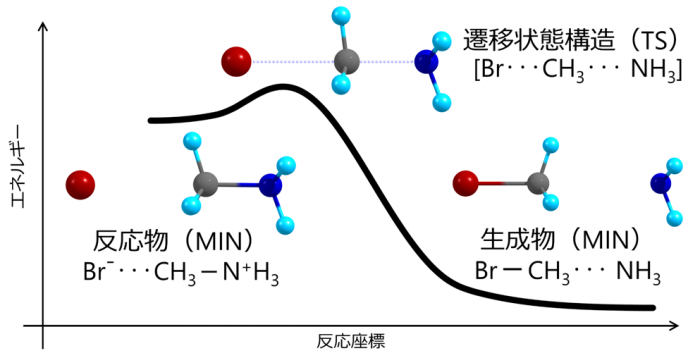
図1 代表的な有機反応(SN2反応)の反応経路に沿ったエネルギープロファイル。
近年開発が進められている反応経路自動探索法により、分子の一つの安定構造の情報を入力するだけでポテンシャルエネルギー曲面上に存在する同じ組成の分子の安定構造を系統的に探索することができるようになりました。これによって、すべての固有反応座標が網羅された反応経路ネットワーク(図2)の作成が可能となり、さまざまな化学反応の機構解明や新しい材料の探索に応用されています。
量子化学計算では化学反応の機構をポテンシャルエネルギー曲面に基づいて議論するため、反応における分子の動的効果(反応ダイナミクス)が考慮されません。反応ダイナミクスは、分子の運動の効果をあらわに考慮するab initio分子動力学法(※2)により調べることができます。ab initio分子動力学法とは、量子化学計算によって原子にはたらく力を求め、ニュートンの運動方程式を解くことで原子座標と速度の時間発展を追跡する手法であり、分子がポテンシャルエネルギー曲面上を運動するときの軌跡(古典軌道)を得ることができます。筆頭著者はこれまで、古典軌道を反応経路ネットワーク上にマッピングする新しい解析手法の開発に取り組んできました。IRCは、分子系から運動エネルギーを取り除いたときにたどるポテンシャルエネルギー曲面上の最急降下経路として定義される反応経路であるため、ダイナミクスの効果を考慮すると分子系は必ずしも固有反応座標に沿って運動するとは限りません。本手法を金5量体の構造変化に適用し、200本の古典軌道を反応経路ネットワークに基づいて解析したところ、114本の古典軌道において分子系が固有反応座標から別の固有反応座標に乗り移る描像(※3)が得られました。
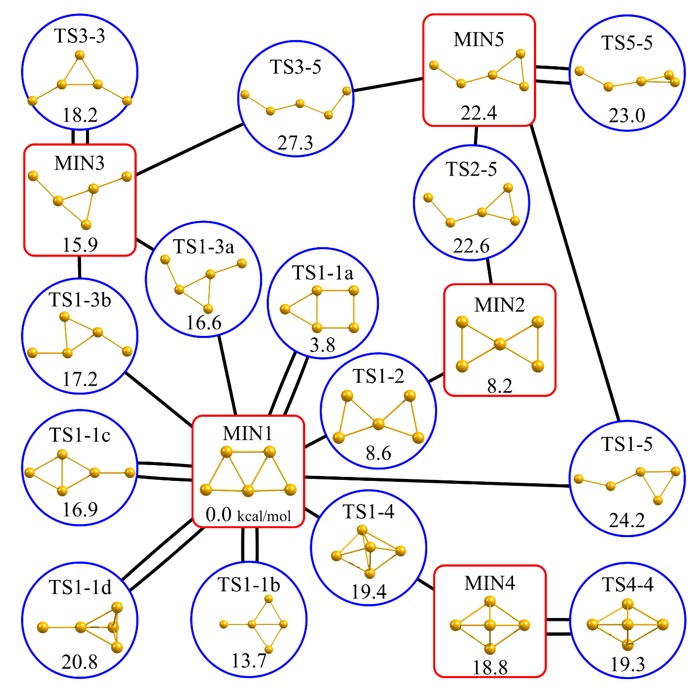
図2 金5量体の反応経路ネットワーク。赤枠、青枠はそれぞれ安定構造、遷移状態構造に対応し、黒線が固有反応座標(IRC)に対応します。すべての遷移状態構造は固有反応座標(IRC)によって遷移状態構造を介して結ばれています。
▮ 着想に至った経緯・数理連携の意義
反応経路ネットワーク上に古典軌道を可視化するには、各安定構造、遷移状態構造の相対的な位置関係がポテンシャルエネルギー曲面上の配置と対応している必要があります。しかし従来の反応経路ネットワークでは、安定構造および遷移状態構造が化学的直観や可視性を考慮して配置されていました。したがって、古典軌道を反応経路ネットワーク上に可視化する解析ではネットワークにおける構造の配置に根拠がないことが問題点であり、学会発表などでも数多くの質問を受けていました。
この問題を解決するために、本リーディングプログラムの異分野ラボビジットを活用し、理学研究院数学部門 荒井迅准教授(現中部大学創発学術院教授)の下でポテンシャルエネルギー曲面の形状を数学的に取り扱う方法論について学びました。修士二年次に実施されたQualifying Examination 1(QE1)では数理連携課題に取り組み、荒井先生と議論を重ねながら本論文の土台となる古典的多次元尺度構成法による反応経路ネットワークの可視化を提案しました。本プログラムの数理連携カリキュラムを活用し、情報統計学と関連が深い数理科学分野との融合研究を進めることで、これまで解決方法を模索していた問題に対する新しい切り口が得られたと感じています。
▮ 研究成果
古典的多次元尺度構成法(主座標分析)とは、多次元データを各データ間の距離関係(類似度)ができるだけ保つように低次元化する手法であり、心理学実験や生態学実験などのデータ解析に用いられています。本研究では、反応経路ネットワークにおいてN原子分子の二つの構造間の3N次元座標の間の直線距離を算出し、古典的多次元尺度構成法を適用することで3N-6次元空間において定義される反応経路ネットワークをより低い次元へ落とし込みました。また、低次元化によって失われた情報量を評価するために累積寄与率を算出しました。累積寄与率とは、低次元化されたネットワークが持つ情報量の割合であり、値が大きいほど3N-6次元空間における情報が保たれていることを示しています。
本論文では、IRCに特徴があることが知られている2つの化学反応への適用例と19の構造を含む反応経路ネットワークへの適用例を報告しました。IRCへの適用では、9原子分子(3N-6=21次元)の素反応と7原子分子(3N-6=15次元)の素反応について、それぞれ二次元空間に可視化しました。累積寄与率はそれぞれ99.7%、95.2%と計算され、IRCの情報が二次元においても十分に保たれていることがわかりました。一方、反応経路ネットワークに対する適用例では、5個のMINと14個のTSから構成される金5量体(3N-6=9次元)の反応経路ネットワークを2次元及び3次元空間に可視化しました。累積寄与率はそれぞれ66.6%、80.9%であり、反応経路ネットワークを9次元から2次元へ落とし込んだ場合でも66.6%の情報が保持されていることがわかりました。このことから、反応経路ネットワークに数理科学的手法を適用することで構造間の相対的な位置関係が考慮された反応経路地図の作成が可能なことが示されました。
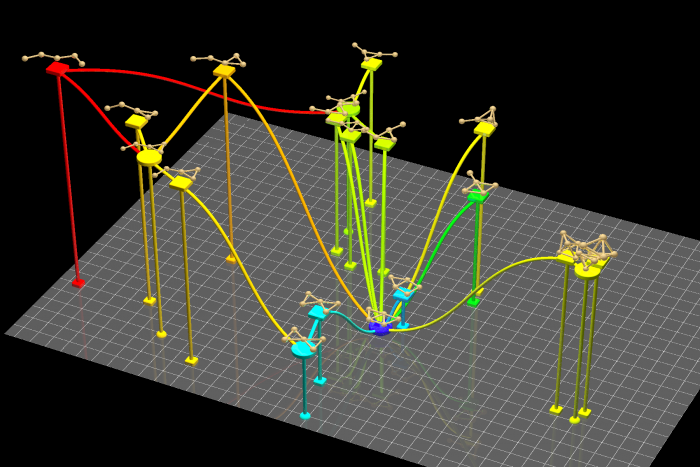
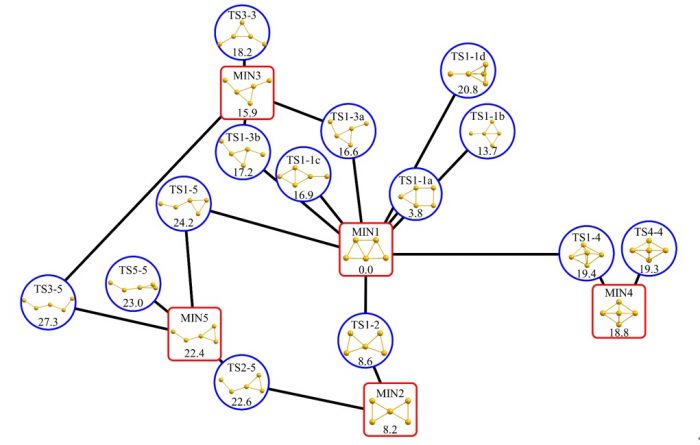 図3 古典的多次元尺度構成法によって得られた金5量体の反応経路地図。
図3 古典的多次元尺度構成法によって得られた金5量体の反応経路地図。
▮ 社会的意義・今後の予定
本研究によって得られた反応経路地図はポテンシャルエネルギー上の安定構造や遷移状態構造の位置関係が可能な限り保たれており、ab initio分子動力学計算から得られる古典軌道を記述する上で意味のある地図になっています。筆頭著者らがこれまでに開発してきた古典軌道マッピング法と本手法を組み合わせることにより、反応経路ネットワークと反応ダイナミクスの双方から化学反応を議論し、化学反応機構に関するより深い洞察が得られます。
▮ 論文情報
研究論文名:Visualization of the Intrinsic Reaction Coordinate and Global Reaction Route Map by Classical Multidimensional Scaling
著者:堤拓朗、小野ゆり子、荒井迅、武次徹也
公表雑誌:Journal of Chemical Theory and Computation 2018, 14 (8), pp 4263–4270 (2018年7月12日Web公開)
DOI番号:10.1021/acs.jctc.8b00176
▮ 付記(科研費や助成金)
本研究は北海道大学物質科学フロンティアを開拓するAmbitiousリーダー育成プログラムならびに日本学術振興会 特別研究員奨励費による助成を受け研究を行いました。
▮ 用語解説
※1 固有反応座標(IRC: intrinsic reaction coordinate):ノーベル化学賞受賞者の福井謙一によって数学的に定義された反応経路であり、ポテンシャルエネルギー曲面において遷移状態構造(TS)を介して2つの安定構造(MIN)を結ぶ最小エネルギー経路として定義されています。
※2 ab initio分子動力学(AIMD: ab initio molecular dynamics)法:分子動力学法とは、各原子にはたらく力に基づきNewtonの運動方程式を解くことで原子座標と速度を時間発展させる手法です。原子座標を時間発展させた後、電子状態計算によりエネルギー勾配を求め、Newtonの運動方程式を解く操作を繰り返し行うことで、原子座標と速度の時系列データである古典軌道が得られます。エネルギーの見積もりには力場を利用する方法と量子化学計算を用いる方法があります。ab initio分⼦動⼒学法は量⼦化学計算から得られるエネルギー
※3 ある反応経路から他の反応経路に乗り移るような描像:筆頭著者は、先行研究でTS1-1d(図2左下)から200本の古典軌道を計算し、古典軌道が辿る経路を反応経路ネットワークに基づいて解析を行いました。200本の古典軌道のうち、86本はTS1-1dからIRCに沿ってMIN1(図2中央)に到達しました。これはIRCに沿った古典軌道です。一方、残りの114本の古典軌道はTS1-1dから他のIRCに近づいてMIN1に到達しました。114本の古典軌道のうち、62本の古典軌道はTS1-1dからTS1-3aに近づきながらMIN1に到達しました。これらは、分子が持つ運動エネルギーの効果によってIRCから逸れ、他のIRCに乗り移った古典軌道であるといえます。(T. Tsutsumi, Y. Harabuchi, Y. Ono, S. Maeda, and T. Taketsugu, Phys. Chem. Chem. Phys., 2018, 20, 1364-1372.)

