本プログラムでは、幅広い知識と考え方を身につける教育の一環として、異分野の研究室にて新しい専門的知識や技術を習得するために「異分野ラボビジット」を実施しています。自身の研究と異分野との関係性を考察して俯瞰力を養成する機会であると同時に、博士前期課程２年次の夏に行われる「Qualifying Examination 1 」の課題選択にもつなげることを目的としています。平成28年度は16名のプログラム3期生が３週間から3か月程度の期間、異なる分野の研究室に移籍し、移籍先研究室が提供する教育研究内容に取り組みました。今回の活動報告では、２名のプログラム生のレポートを紹介します。

●新しいアイディアを獲得できた 1ヶ月の移籍●
報告：リーディングプログラム3期生　金 容俊
【移籍先】総合化学院 生物化学研究室
【所　属】総合化学院 有機金属化学研究室
【期　間】平成28年11月28日ー12月26日

私は所属している有機金属化学研究室（総合化学院）で、新しいホスフィン配位子の合成および応用について研究しています。有機合成分野の知識だけでは得られがたい新しいアイディアを獲得するため、異分野ラボビジット先として生物化学研究室（総合化学院）を選び、1ヶ月間移籍しました。生物化学研究室では、多種類のアミノ酸の縮合で多様な構造を作り、多様な機能を生み出すタンパクおよびペプチドを勉強しました。目的とした配列を持つペプチドを大腸菌を用いて培養し精製することを学び、作ったペプチドをバイオミネラリゼーションに用いて銀ナノ粒子を作りました。得られた銀ナノ粒子を観察し、多量体化バイオミネラリゼーションペプチドの銀ナノ構造体形成への効果について考察することもできました。

生物化学研究室での1ヵ月間、所属研究室での研究とは全く異なる研究をしました。非常に勉強になっただけでなく、実験をひと区切り終わらせることもできました。自分の力だけでは絶対にできなかったことでしたが、生物化学研究室の皆さんが優しく積極的に教えてくださり、知らないことがあればすぐ聞くことができました。お世話になった生物化学研究室のメンバーに感謝しています。

 

●数学の視点から自身の研究を見つめ直すことができた異分野ラボビジット●
報告：リーディングプログラム3期生　堤 拓朗
【移籍先】理学研究院数学部門 荒井研究室
【所　属】総合化学院 量子化学研究室
【期　間】平成28年11月4日－平成29年1月27日

数学の概念を身につけることが理論化学者として重要であると私は考えています。そのため修士課程進学後から理学部数学科の講義を聴講し、数学に触れる機会を増やしてきました。また、所属する量子化学研究室では、第一原理分子動力学計算によって得られた結果を統一的に解析する手法を開発しています。研究では、5原子分子によって形成される9次元のポテンシャルエネルギー超曲面という人間では想像できない多次元空間を扱っています。開発の段階で、9次元空間に存在する極小点や極大点によって形成されるネットワークを、できるだけ直観的に2次元地図で表現したいという課題に直面していました。そこで、私は数学の視点から自分自身の研究を見つめ直し、新しい可視化法を生み出したいという想いから、計算トポロジーの概念をポテンシャルエネルギー超曲面に応用している理学研究院数学部門の荒井研究室を異分野ラボビジット先に選びました。荒井研究室では、トポロジーに関する考え方の取得のため松本幸夫著『岩波講座 現代数学の基礎 Morse理論の基礎』を読み、関数の性質から空間の形を調べることができるMorse理論に関するゼミを毎週実施しました。ゼミは私が参考書を読み、理解したことを板書してまとめるという形式で、「曲面上の臨界点の性質とHesse行列の定義」「Morseの補題の概要」「Morse関数と曲面の形状の関係」「ハンドル分解」について学び、理解しました。

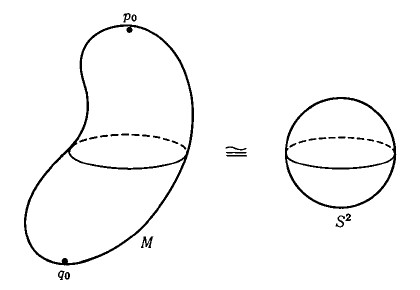
図: Morse関数と曲面の形状の関係。臨界点が2つ（点p0と点q0）だけ持つMorse関数が存在する閉曲面
　（左）と球面（右）はトポロジー的に同じ形である（微分同相である）。
　 出典　松本幸夫『岩波講座現代数学の基礎　Morse理論の基礎』（岩波書店、1997）

このたびの異分野ラボビジットを通じて、Morse理論の理解のために必要な数学の予備知識とMorse理論によって空間がどのように表現できるかということについて学習しました。Morse理論についてさらに学ぶことで、自身の研究に対する理解が深まると感じました。今後は自身の研究とMorse理論を結びつけ、QE1 で数理連携の研究提案が行えるよう準備を進めていきたいです。

報告：金 容俊（リーディングプログラム3期生）
　　　堤 拓朗（リーディングプログラム3期生）
構成：リーディングプログラム事務局工学分室